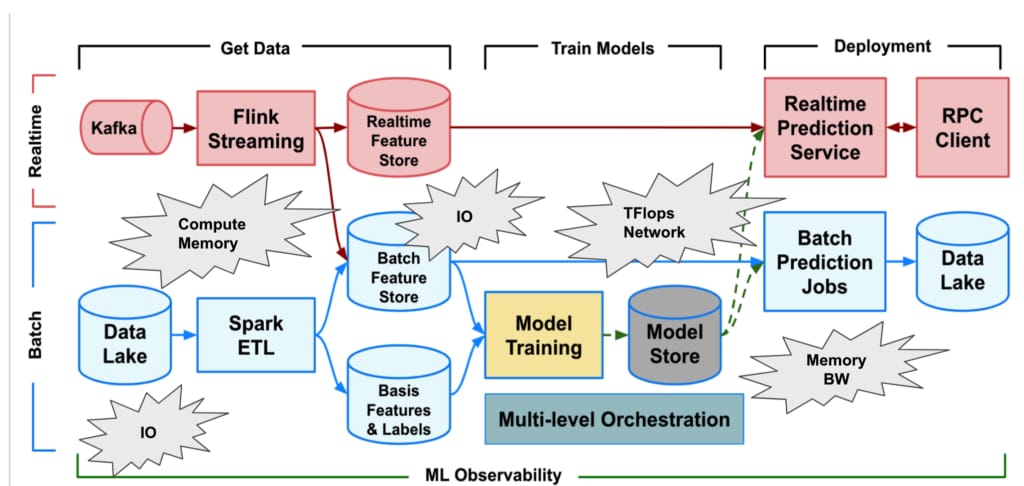
Tools that enable fast and flexible experimentation democratize and accelerate machine learning research. Take for example the development of libraries for automatic differentiation, such as Theano, Caffe, TensorFlow, and PyTorch: these libraries have been instrumental in catalyzing machine learning research, enabling gradient descent training without the tedious work of hand-computing derivatives. In these frameworks, it’s simple to experiment by adjusting the size and depth of a neural network, by changing the error function that is to be optimized, and even by inventing new architectural elements, like layers and activation functions–all without having to worry about how to derive the resulting gradient of improvement.
One field that so far has not been greatly impacted by automatic differentiation tools is evolutionary computation. The reason is that most evolutionary algorithms are gradient-free: they do not follow any explicit mathematical gradient (i.e., the mathematically optimal local direction of improvement), and instead proceed through a generate-and-test heuristic. In other words, they create new variants, test them out, and keep the best.
Recent and exciting research in evolutionary algorithms for deep reinforcement learning, however, has highlighted how a specific class of evolutionary algorithms can benefit from auto-differentiation. Work from OpenAI demonstrated that a form of Natural Evolution Strategies (NES) is massively scalable, and competitive with modern deep reinforcement learning algorithms. Follow-up work from Uber AI focused on highlighting fundamental properties of NES (for instance, how it relates to traditional gradient descent), adding novelty-based exploration to improve NES’s performance, and leveraging NES to create scalable open-ended evolutionary algorithms. NES is distinct from traditional evolutionary methods, because each generation of NES’s evolution seeks to follow an explicit mathematical gradient.
To more easily prototype NES-like algorithms, Uber AI researchers built EvoGrad, a Python library that gives researchers the ability to differentiate through expectations (and nested expectations) of random variables, which is key for estimating NES gradients. The idea is to enable more rapid exploration of variants of NES, similar to how TensorFlow enables deep learning research. We believe there are many interesting algorithms yet to be discovered in this vein, and we hope this library will help to catalyze progress in the machine learning community. Beyond EvoGrad, this blog post also announces Evolvability ES, a new NES-based meta-learning algorithm developed by Uber AI researchers that precipitated the creation of EvoGrad.
Natural evolution strategies
Before describing NES, it’s useful to review how evolutionary algorithms usually work. Traditional evolutionary algorithms subject a population (an evolving collection of potential solutions that are explored in parallel) to a heuristic survival-of-the-fittest competition. Individuals that score higher on the fitness function (the objective function guiding search) are granted more offspring in the next generation (slightly perturbed copies of themselves or combinations of themselves with other individuals). In contrast, individuals that score poorly are removed from the population.
NES imposes a formal probabilistic structure on evolution. Instead of viewing a population as a finite list of individuals, NES abstracts the population as a probability distribution over the search space, which is often a Gaussian distribution centered around a single set of parameters. Individuals can then be sampled from this distribution (in effect by adding Gaussian perturbations to the center of the population) and evaluated. In this view, a population becomes a probabilistic cloud, reflecting the intuition that in any evolutionary population, generating some new individuals is more likely than generating others (for instance, mutation might be more likely to change your eye color than to give you wings). The objective of NES is to iteratively update this population distribution such that the average fitness of individuals drawn from the population is maximized—in other words, to keep moving the population cloud towards greener pastures (visualized here).
It turns out that this cloud-improvement objective function can be differentiated, because a population distribution is smooth in a way that a collection of discrete individuals is not. The result is a mathematical formula for an explicit gradient of improvement, one that can be estimated by evaluating samples from the population; not surprisingly, sampling more individuals yields a better gradient estimate. This can be viewed as integrating the information from all samples to decide the best direction to move the population cloud, somewhat like a mating operation that combines the best of all individuals. The exciting benefit is that with enough samples, the algorithm is guaranteed to gradient-follow in a similar way to stochastic gradient descent (which we know from deep learning research is a powerful tool), even though the problem evolution is solving may be non-differentiable!
Importantly, the symbolic form of this gradient estimation must be separately derived for different choices of representing the population distribution (e.g., Gaussian with fixed variance, Gaussian with learned covariance, Cauchy, or mixture models, to name a few options) and on what metric of the population is to be optimized (e.g., average fitness, maximum fitness, or the diversity of expressed behaviors as in Evolvability ES, which we describe later in this post). Performing such derivations by hand can be tedious and requires specific mathematical knowledge, which slows down the pace of NES research.
Introducing the EvoGrad Library
In this project, we have made a simple Python library called EvoGrad for prototyping NES-like algorithms, using PyTorch as a backend. The main feature EvoGrad provides is the ability to differentiate through expectations of random variables (and nested expectations, extending work by others on stochastic computation graphs), which is key for estimating NES gradients (because NES aims to maximize the expected fitness across the population distribution).
We created this library while developing a new form of NES called evolvability ES, which is driven to evolve a population that exhibits maximally diverse behaviors. The idea is that such a population could be a storehouse of evolutionary adaptations, readily adaptable to new situations. This kind of model is often useful in meta-learning, a growing subfield of machine learning focusing on learning how to learn. In the following section, we’ll build up to introducing this evolvability ES algorithm through a set of EvoGrad examples.
A simple example: implementing NES
As a first example, we’ll implement the simplified NES algorithm of Salimans et al. (2017) in EvoGrad. EvoGrad provides several probability distributions which may be used in the expectation function. We will use a normal distribution because it is the most common choice in practice.
Let’s consider the problem of finding a fitness peak in a simple 1-D search space.
We can define our population distribution over this search space to be initially centered at 1.0, with a fixed variance of 0.05, with the following Python code:
mu = torch.tensor(1.0, requires_grad=True)
p = Normal(mu, 0.05)
Next, let’s define a simple fitness function that rewards individuals for approaching the location 5.0 in the search space:
def fitness(xs):
return -(x – 5.0) ** 2
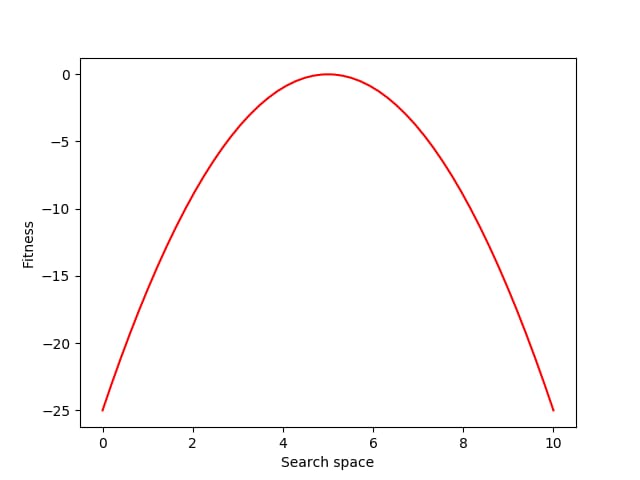
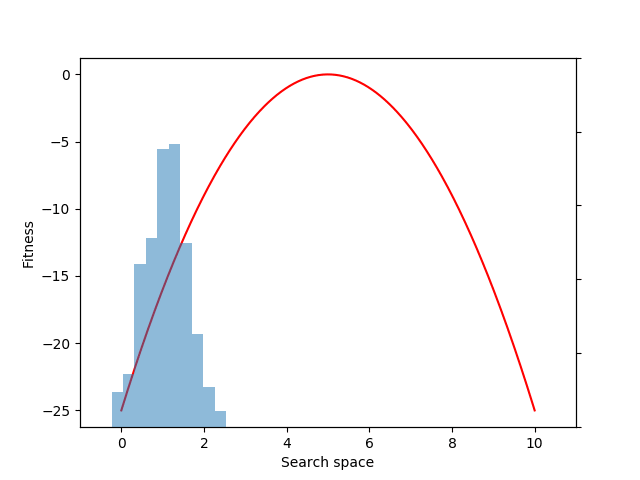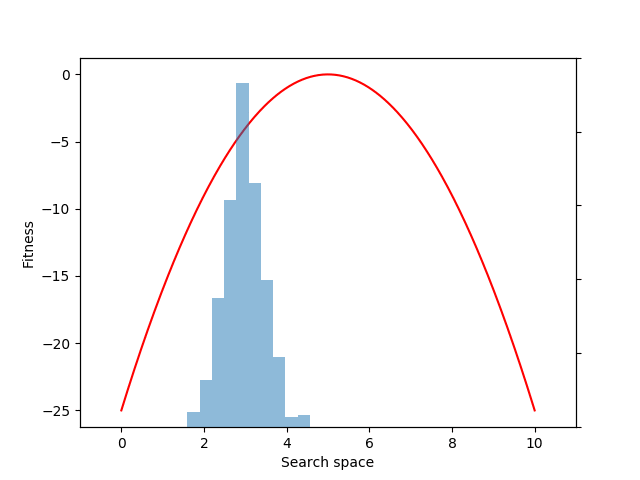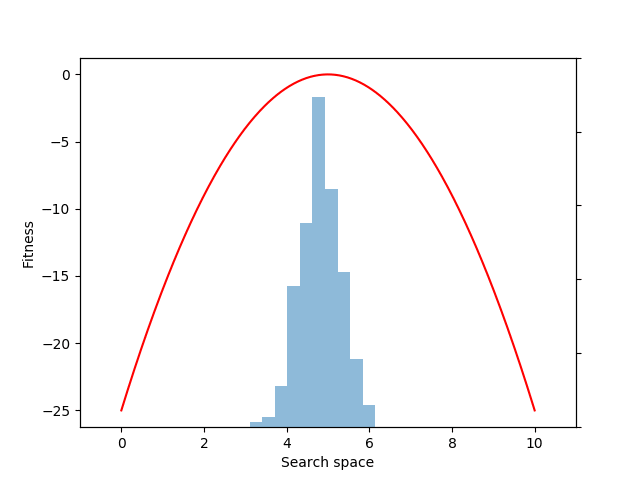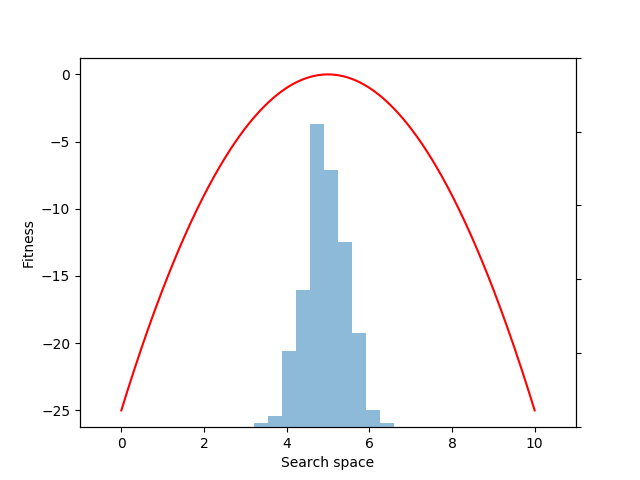
Each generation of evolution in NES takes samples from the population distribution and evaluates the fitness of each of those individual samples. Here we sample and evaluate 100 individuals from the distribution:
sample = p.sample(n=100)
fitnesses = fitness(sample)
Optionally, we can apply a whitening transformation to the fitnesses (a form of pre-processing that often increases NES performance), like this:
fitnesses = (fitnesses – fitnesses.mean()) / fitnesses.std()
Now we can use these calculated fitness values to estimate the mean fitness over our population distribution:
mean = expectation(fitnesses, sample, p=p)
Although we could have estimated the mean value directly with the snippet: mean = fitnesses.mean(), what we gain by instead using the EvoGrad expectation function is the ability to backpropagate through mean. We can then use the resulting auto-differentiated gradients to optimize the center of the 1D Gaussian population distribution (mu) through gradient descent (here, to increase the expected fitness value of the population):
mean.backward()
with torch.no_grad():
mu += alpha * mu.grad
mu.grad.zero_()
Another example: maximizing the variance of behaviors in the population
As a more sophisticated example, rather than maximizing the mean fitness, we can maximize the variance of behaviors in the population. While fitness is a measure of quality for a fixed task, in some situations we want to prepare for the unknown, and instead might want our population to contain a diversity of behaviors that can easily be adapted to solve a wide range of possible future tasks.
To do so, we need a quantification of behavior, which we can call a behavior characterization. Similarly to how you can evaluate an individual parameter vector drawn from the population distribution to establish its fitness (e.g. how far does this controller cause a robot to walk?), you could evaluate such a draw and return some quantification of its behavior (e.g., what position does a robot controlled by this neural network locomote to?).
With this idea of behavior, we can then seek out the point in the population’s parameter space where the resulting population distribution contains the widest diversity of behaviors. This is the aim of evolvability ES, and is made easier by the autodifferentation capabilities of EvoGrad.
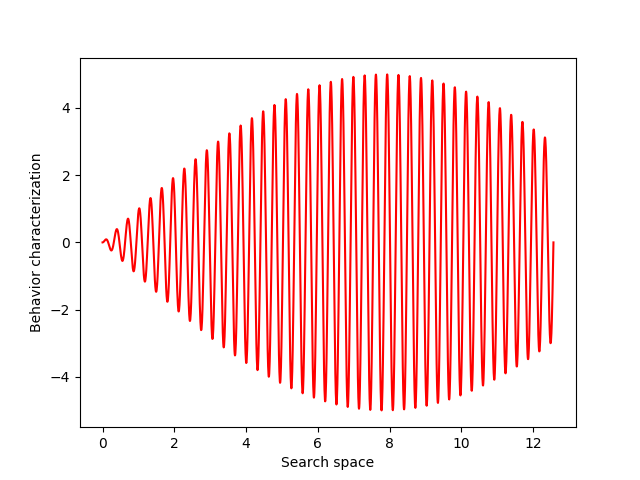
For this example, let’s choose a simple but illustrative, 1D behavior characterization, namely, the product of two sine waves (one with much faster frequency than the other):
def behavior(x):
return 5 * torch.sin(0.2 * x) * torch.sin(20 * x)
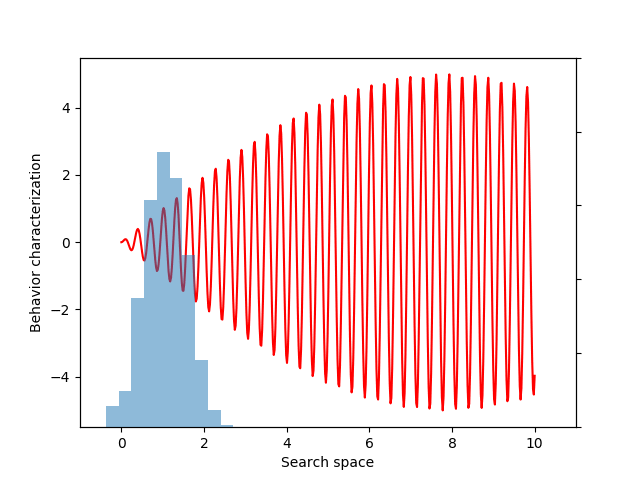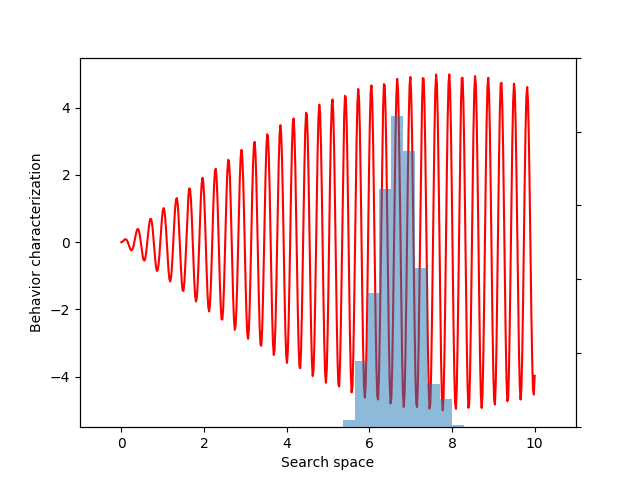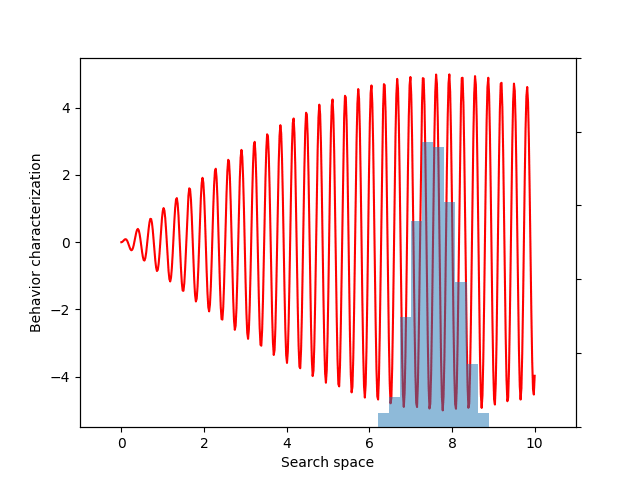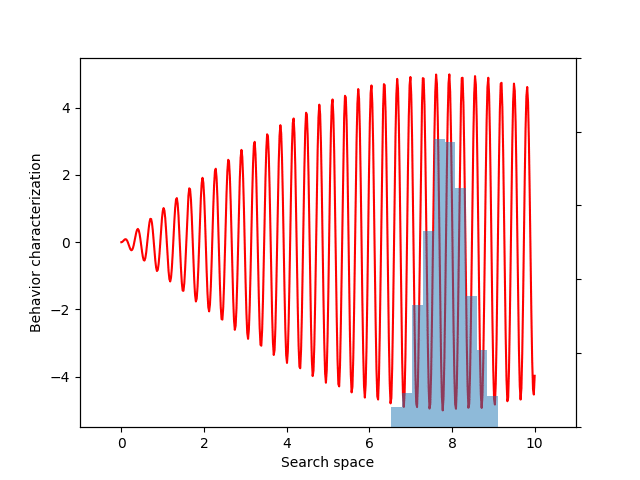
Now, instead of estimating the mean fitness, we can calculate a statistic that reflects the diversity of sampled behaviors. The variance of a distribution is one metric of diversity, and one variant of evolvability ES measures and optimizes such variance of behaviors sampled from the population distribution:
sample = p.sample(n=100)
behaviors = behavior(sample)
zscore = (behaviors – behaviors.mean()) / behaviors.std()
variance = expectation(zscore ** 2, sample, p=p)
This variance variable can then be used during optimization, as before. The animation below shows the progress of such optimization, which correctly uncovers the most evolvable behavior.
A final example: maximizing the entropy of behaviors
In the previous example, the gradient would be relatively straightforward to compute by hand. However, sometimes we may need to maximize objectives whose derivatives would be much more challenging to derive. In particular, this final example will seek to maximize the entropy of the distribution of behaviors (a variant of evolvability ES). We believe entropy is a more principled measure of diversity, because entropy is maximized by uniform coverage of all possible behaviors.
To create a differentiable estimate of entropy, we first compute the pairwise distances between the different behaviors. Next, we create a smooth probability distribution by fitting a kernel density estimate:
dists = scipy.spatial.distance.squareform(scipy.spatial.distance.pdist(behaviors, “sqeuclidean”))
kernel = torch.tensor(scipy.exp(-dists / k_sigma ** 2), dtype=torch.float32)
p_x = expectation(kernel, sample, p=p, dim=1)
Then, we can use these probabilities to estimate the entropy of the distribution, and run gradient descent on it as before:
entropy = expectation(-torch.log(p_x), sample, p=p)
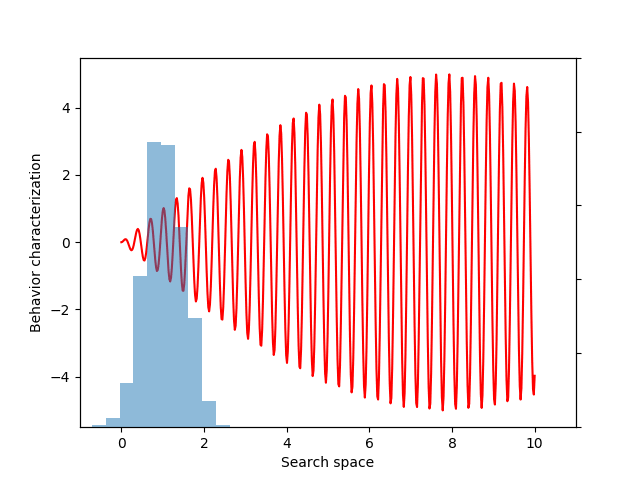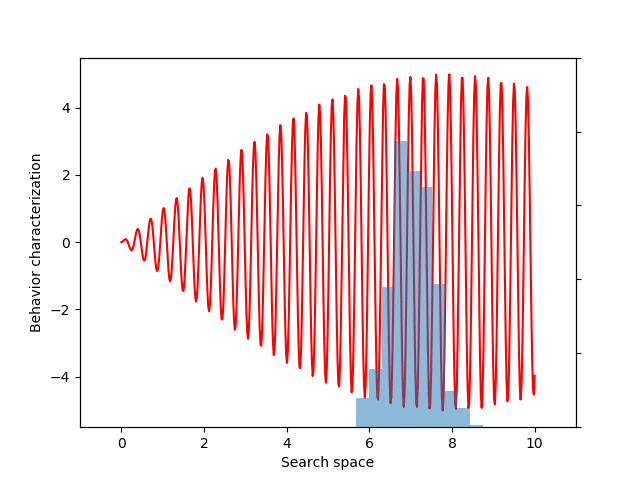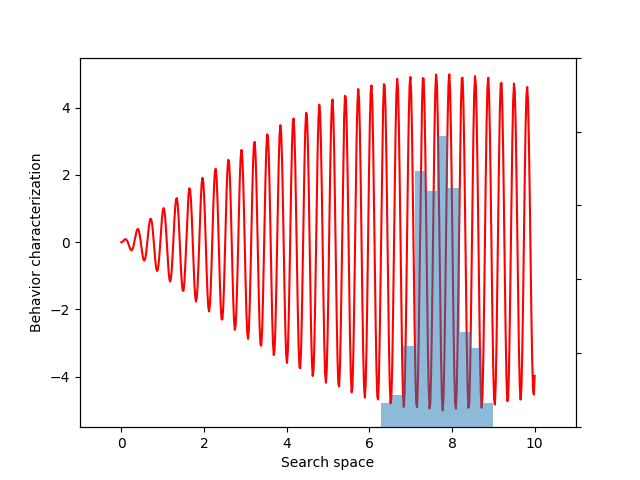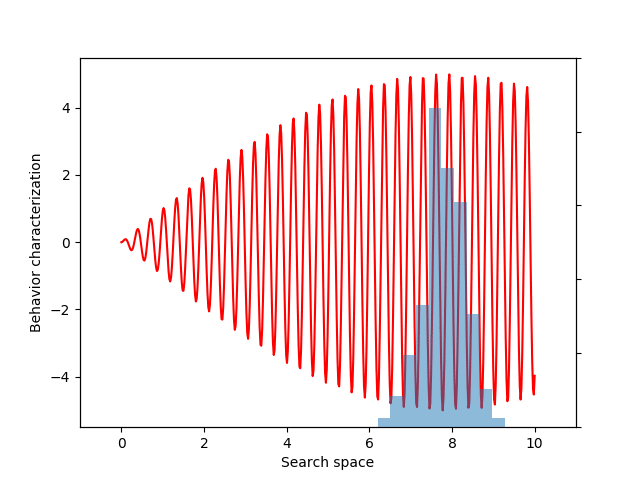
If you don’t follow the exact details of the entropy calculation, the most important point is that EvoGrad enables differentiating through the whole procedure, enabling much easier exploration of new algorithms. The software package and this demo code can be found on our GitHub repository.
Evolvability ES: scalable generation of evolvable populations
Complementing the release of this library, we published a paper, accepted at the GECCO academic conference, describing evolvability ES, the work that motivated us to create the EvoGrad library. A longstanding goal in evolutionary computation (the study of algorithms inspired by biological evolution) is to create algorithms that generate evolvable solutions (in other words, solutions able to rapidly adapt to new challenges).
Animal species have an impressive ability to evolutionarily adapt. Take the incredible diversity of dogs, for example, which humans bred from wolves in relatively short order. We want the same kind of adaptive abilities to result from our machine learning algorithms, both because training new solutions from scratch is expensive and because real-world tasks often shift and change over time. However, while such evolvability is common in natural evolution, it remains challenging for evolutionary algorithms, like NES, to produce.
While there are other interesting approaches for generating evolvability, evolvability ES is a new, efficient, and scalable algorithm for directly optimizing evolvability. The main idea is to apply modified versions of NES (as detailed in the last two examples above) that maximize the diversity of behaviors in a single evolved population. In effect evolvability ES seeks out highly-evolvable parts of the search space, where slight perturbations of a central parameter vector give highly divergent behaviors (and can be seen as an evolutionary adaptation of the popular MAML meta-learning algorithm—see our paper for further discussion of this point). The resulting algorithm is easy to parallelize and benefits from following an approximate gradient of diversity maximization. EvoGrad was integral to the development of evolvability ES because of the automatic differentiation through expectation that the library enables (in that it allowed us to rapidly test the ideas presented here and many others).
In one experiment detailed in our research paper, evolvability ES evolved a population of neural network controllers for a simulated four-legged robot that encoded diverse walking behaviors. While NES would typically uncover a single highly-performing behavior, evolvability ES instead finds a repertoire of behaviors that efficiently walk in all different directions, all produced by perturbing one central parameter vector! To get an idea of what this looks like in practice, the video below shows two behaviors produced by perturbing the same parameter vector.
In addition, the animation below shows how, over generations of evolution, the behaviors demonstrated by the population (i.e. perturbations of the central parameter vector) in evolvability ES become better adapted to the task of walking in diverse directions:
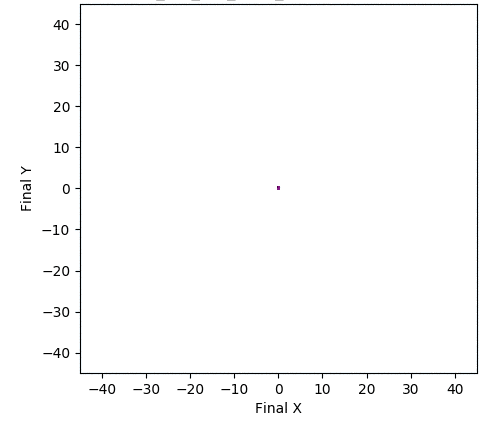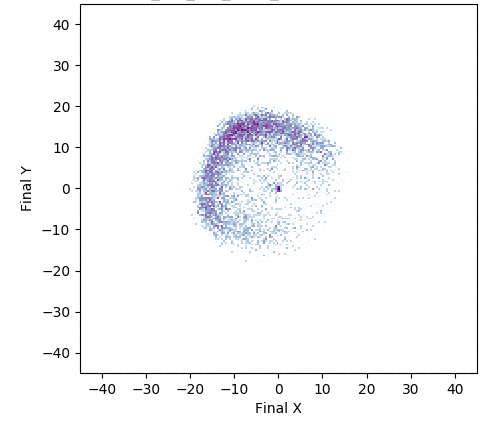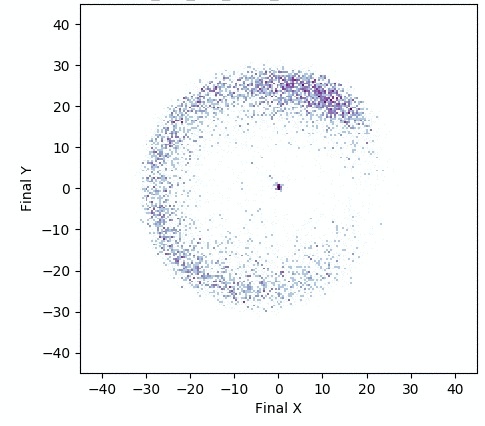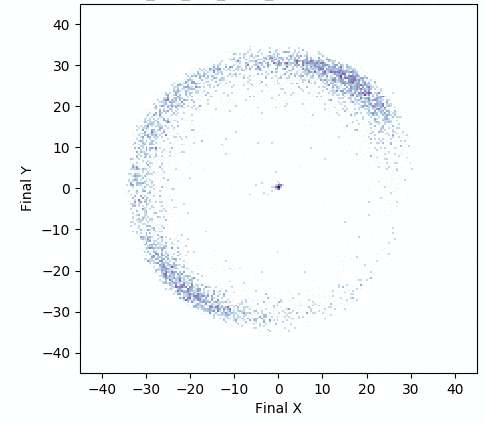
One intriguing fact these results highlight is that there exist highly-evolvable regions of parameter space for deep neural networks, wherein small random perturbations of parameters result in highly divergent, yet well-adapted behaviors (here, behaviors that walk in many directions). This echoes (and in effect goes a step beyond) similarly-inspired work with MAML, where a parameter vector is discovered that can quickly adapt to new tasks with additional steps of gradient descent.
We believe this is an exciting (and unexpected) result, and future work on evolvability ES through EvoGrad and other libraries could further explore more complex multi-modal population distributions and combinations with more expressive genetic encodings.
Moving forward
Beyond the evolvability ES algorithm that motivated EvoGrad, we believe there are many other NES-like algorithms left to be created and explored through this package. Particularly interesting are hybrids of NES (or other evolutionary algorithms) with standard gradient-based search, which can exploit both the flexibility of evolution (e.g. to deal with non-differentiable problem domains) and the efficiency of deterministic gradients.
EvoGrad source code is shared under a non-commercial license for research purposes only.
This work was led by Alex Gajewski, an undergraduate summer research intern with AI Labs. If working on machine learning research like this excites you, learn more about our internship programs.

Alex Gajewski
Alex Gajewski is a third-year undergrad at Columbia University studying math and computer science, and was as a summer 2018 intern with Uber AI. He is excited by the potential of emerging technologies like machine learning to change the ways we interact with each other and ourselves.

Jeff Clune
Jeff Clune is the former Loy and Edith Harris Associate Professor in Computer Science at the University of Wyoming, a Senior Research Manager and founding member of Uber AI Labs, and currently a Research Team Leader at OpenAI. Jeff focuses on robotics and training neural networks via deep learning and deep reinforcement learning. He has also researched open questions in evolutionary biology using computational models of evolution, including studying the evolutionary origins of modularity, hierarchy, and evolvability. Prior to becoming a professor, he was a Research Scientist at Cornell University, received a PhD in computer science and an MA in philosophy from Michigan State University, and received a BA in philosophy from the University of Michigan. More about Jeff’s research can be found at JeffClune.com

Kenneth O. Stanley
Before joining Uber AI Labs full time, Ken was an associate professor of computer science at the University of Central Florida (he is currently on leave). He is a leader in neuroevolution (combining neural networks with evolutionary techniques), where he helped invent prominent algorithms such as NEAT, CPPNs, HyperNEAT, and novelty search. His ideas have also reached a broader audience through the recent popular science book, Why Greatness Cannot Be Planned: The Myth of the Objective.

Joel Lehman
Joel Lehman was previously an assistant professor at the IT University of Copenhagen, and researches neural networks, evolutionary algorithms, and reinforcement learning.
Posted by Alex Gajewski, Jeff Clune, Kenneth O. Stanley, Joel Lehman
Related articles
Most popular

How Uber Serves Over 40 Million Reads Per Second from Online Storage Using an Integrated Cache

Ensuring Precision and Integrity: A Deep Dive into Uber’s Accounting Data Testing Strategies

Building Scalable, Real-Time Chat to Improve Customer Experience

Network IDS Ruleset Management with Aristotle v2
Products
Company