This article is the second in our series dedicated to highlighting causal inference methods and their industry applications. Previously, we published an article on mediation modeling, which is one of many methods within the broader category of causal inference. In future articles, we plan on discussing some initiatives at Uber to scale causal inference methods through our platform and tools.
At Uber Labs, we apply behavioral science insights and methodologies to help product teams improve the Uber customer experience. One of the most exciting areas we’ve been working on is causal inference, a category of statistical methods that is commonly used in behavioral science research to understand the causes behind the results we see from experiments or observations. We’ve found it invaluable to bring causal inference methods to our work at Uber, as it enables us to solve challenging but critical data science questions that would otherwise be impossible to tackle, such as estimating the treatment effect when a randomized controlled experiment is not possible or addressing additional complexities within the experimental data.
Teams across Uber apply causal inference methods that enable us to bring richer insights to operations analysis, product development, and other areas critical to improving the user experience on our platform.
What is causal inference?
Causal inference consists of a family of statistical methods whose purpose is to answer the question of “why” something happens. Standard approaches in statistics, such as regression analysis, are concerned with quantifying how changes in X are associated with changes in Y. Causal inference methods, by contrast, are used to determine whether changes in X cause changes in Y. Therefore, unlike methods that are concerned with associations only, causal inference approaches can answer the question of why Y changes. If X is causally related with Y, then Y’s change can be explained in terms of X’s change.
Humans have been interested in causality for hundreds of years. However, causal inference as a family of methodologies is a fairly new development, as researchers didn’t used to have formal networks of causal relations.1 This only changed in the latter half of the 20th century thanks to the work of pioneering methodologists such as Donald Rubin and Judea Pearl.2,3,4
In recent years, the field of causal inference has grown in scope and impact. We now have more and better methodologies for answering “why” questions. Causal inference methods have improved the analysis of experiments at Uber, quasi-experiments, and observational data. Causal inference is now making inroads to machine learning and artificial intelligence, with pioneers in the field pointing to it as an increasingly significant research area.
Why is causal inference important?
At a high level, causal inference helps us provide a better user experience for customers on the Uber platform. The insights from causal inference can help identify customer pain points, inform product development, and provide a more personalized experience. For example, if we know that users are submitting customer support tickets due to a lack of clarity around how to use a new feature and not dissatisfaction with the feature itself, we can focus on improving the communications around how to use this feature rather than updating or decommissioning the feature.
In the context of Uber Eats, for instance, if we know that an eater regularly orders certain types of cuisine on the platform, we can make meal recommendations and provide them with the most relevant information.
At a higher level, causal inference provides information that is critical to both improving the user experience and making business decisions through better understanding the impact of key initiatives. For example, if we are able to translate intangible variables such as customer satisfaction to business metrics, we can then use that information to help prioritize new features and tools. If we are able to understand the short-term and long-term impact of a new program such as Uber Pro, that will help us build more sustainably and inform future product development decisions.
At a more granular level, causal inference enables data scientists and product analysts to answer causal questions based on observational data, especially when A/B testing is not possible, or gain additional insights from a well-designed experiment. For example, we may launch an email campaign that is open for participation to all customers in a market. In this case, since we don’t have a randomized control group, how do we measure the campaign’s effect? In another example, suppose we have a randomized, controlled A/B test experiment but not everyone in the treatment group actually receive the treatment (i.e., if they don’t open the email). How do we estimate the treatment effect for the treated? Causal inference enables us to answer these types of questions, leading to better user experiences on our platform.
Varieties of causal inference
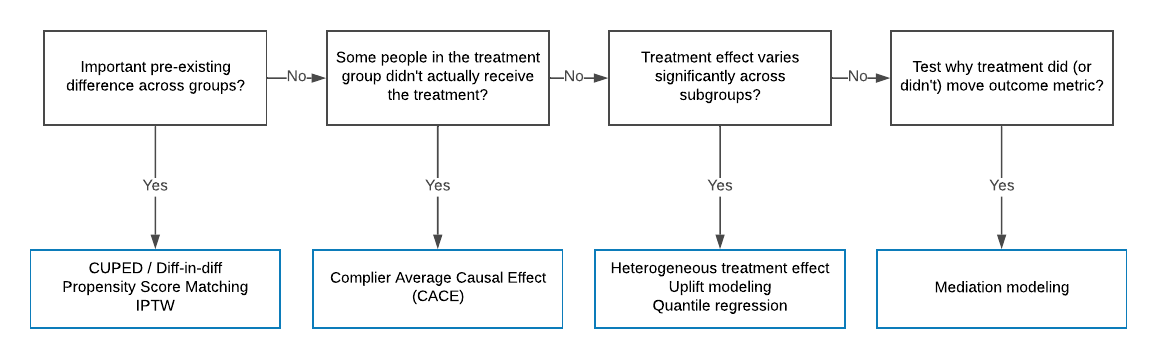
Since causal inference is a family of loosely connected methods, it can feel overwhelming for a beginner to form a structural understanding of the various methods. For a clearer understanding, we’ll divide the methods into two categories: those that are used with experimental data and those that are used with observational data.
These various methods are not mutually exclusive and, quite often, multiple methods can be applied to tackle the same problem. In the flowchart in Figure 1, below (and others throughout the article), we highlight possible solutions for handling given research tasks. Keep in mind that this list is not exhaustive, just a small representation of the type of tactics we use at Uber.
Causal inference with experimental data
Uber’s strong culture of robust and rigorous scientific inquiry helps innovate our products and improve the customer experience. In most cases, randomized controlled experiments (when available) are the cleanest way to demonstrate causality and the estimation of the treatment effect is straightforward. Why would we need to use causal inference when we have an experiment? In many cases, we may not be satisfied with just knowing the average treatment effect. Causal inference enables us to address additional complexities within the experimental data and gives us more insight into how and why the treatment had the effect it did.
When there is pre-existing difference
When a researcher intends to randomly assign people into groups, they may still see some unexpected pre-existing difference between the treatment and control. It may be due to the noisy nature of the field data, such as high variance in the data. To adjust for the pre-existing difference, they can use the controlled-experiment using pre-experiment data (CUPED) method. While this method is often used as a variance reduction technique for online experiments, we’ve found it useful for bias reduction as well.5
When applying the CUPED method, researchers first make predictions of the post-experiment data using the pre-experiment data to estimate what the baseline would be for each individual if there was no treatment. Researchers then adjust the observed post-experiment outcome using the predicted baseline to perform the experiment analysis. This may sound similar to the difference-in-differences approach, a special case of the CUPED method where the coefficient of pre-experiment data in the first model is equal to one. The CUPED method has been implemented at Uber via our internal experiment platform.
Of course, there is a degree to which the randomization fails, causing different levels of pre-existing bias. If the randomization completely fails, researchers could also consider treating the experiment as an observational study, using methods such as propensity score matching or inverse probability of treatment weighting (IPTW).
When some people in the treatment group do not receive the treatment
Imagine a company sends out an email to its customers, but not everyone in the treatment group who got the email actually opened it. How would we estimate the email’s impact? If we only look at those who opened the email in the treatment group and compare them with those in the control group that didn’t get an email, selection bias may arise. Those who chose to open the email may be different from those who didn’t choose to open the email.
To avoid the selection bias, we may compare the control group with the entire treatment group regardless of email opens. However, in that case the estimated effect would be diluted because some of the people in the treatment group were not actually treated. How can we estimate the effect of actually receiving the treatment in an unbiased way?
To address this problem, we can use the complier average causal effect (CACE) approach.6,7 CACE adjusts the intention-to-treat effect (ITT) (i.e., the effect of treatment assignment) with the compliance rate in order to estimate the treatment effect for the subpopulation that is actually being treated.
One can think of CACE in the framework of instrumental variables.7,8 Specifically, in the above email example, imagine that the only way for the random group assignment to influence the outcome variable is through customers actually opening the email. The CACE method requires this assumption. Using CACE methods, researchers can estimate the effect of actually receiving the treatment on the outcome variable by using the group assignment as an instrumental variable.
When treatment effect varies across segments
Companies like Uber serve a variety of customers, each with their own preferences and needs.8,9,10 Consequently, treatment that works well for one group of customers may not work well for another group.11, 12 Among other solutions, the heterogeneous treatment estimation (HTE) method of causal inference enables researchers to identify customized experiences that are optimized to benefit everyone.13, 14 In HTE analysis, researchers calculate the conditional average treatment effect (CATE), which is the treatment effect conditional on observed covariates. The goal of HTE is to identify which segment has the largest delta between treatment and control; in other words, which group of people would benefit the most from the given treatment.
A typical workflow of HTE is to first conduct an A/B test and then use the experiment data to train the HTE model. Researchers can then identify the optimal treatment for different segments based on the results. After that, they run a second experiment with the personalized treatment to validate their ideas.15
There are different ways to estimate HTEs. One popular approach at Uber is called uplift modeling, while quantile regression is another widely-used approach.16
When we want to know why X causes Y
Suppose there is an experiment where the treatment variable X had a significant impact on the outcome variable Y. While we may have a hypothesis about why these two variables are related, in a standard analysis such as regression, the hypothesis is only logically inferred rather than empirically tested with data. Mediation modeling, a causal inference method frequently used at Uber, solves this problem. It opens the black box between a treatment and an outcome variable to reveal the underlying mechanisms (i.e., why something happened).
Essentially, mediation modeling decomposes the total treatment effect into two parts: one that’s due to a particular mechanism we hypothesized (the average causal mediation effect) and the other that’s due to all other mechanisms (the average direct effect). In this way, mediation modeling helps empirically test whether the data supports a causal hypothesis. As illustrated in our previous article on this topic, this type of modeling can be used to directly test product assumptions; compare the relative importance of multiple underlying mechanisms; understand the business impact of intangible variables, such as customer satisfaction; and inform researchers on how to break up a long-term goal into short-term steps.
Causal inference with observational data

While we run a lot of experiments at Uber, we do not want to negatively impact the customer experience with our research. To estimate the causal impact of some variable that hasn’t been randomized, we can leverage observational data rather than data obtained via experimentation.
As an example, we might want to know how experiencing an event like a delay in food delivery can influence Uber Eats customers’ future engagement with the platform. However, since delaying food deliveries would impact the customer experience negatively, we need to use alternative approaches to estimate the impact of such an event.
Examining observational data consisting of users who happened to experience a delayed delivery and users who didn’t, we can begin to understand the impact without resorting to experimentation. However, simply calculating the difference in future customer engagement between these two groups would not likely give us a meaningful answer. The users who have experienced delays may be importantly different from those who haven’t. For example, Figure 3, below, shows one possible causal graph that could be generated from the observed data:

If we were to naively compare the experiences of those whose food deliveries were delayed with those whose weren’t, we might arrive at the implausible conclusion that experiences of delayed deliveries increase customer engagement. But the most plausible explanation is simple: those who are more likely to experience a delayed delivery are likely those who make a larger number of orders, and consequently this group also has higher engagement.
In the graph above, a users’ number of Uber Eats orders represents a back-door path between the treatment variable and outcome of interest.2 In observational causal inference, we try to block such back-door paths. One way we can do this is by controlling for the past Uber Eats orders in our analysis: for instance, only compare those who have, say, five orders from Uber Eats.
Of course, the graph shown in Figure 3, above, represents a simplification. The real data-generating graph could have a bevy of complex back-door paths involving a number of different variables. Determining the variables that should and should not be controlled for is an important step of a causal inference analysis and involves close collaboration between researchers and domain experts who have substantive knowledge of the business problem in question.
Once we have determined the variables that should be included, there are many ways to carry out causal modeling. The simplest way is to only compare treated and non-treated individuals who have the exact same values for the relevant covariates. However, this approach may not be feasible if the number of covariates is large. This is why we usually summarize those covariates in the form of a propensity score, which is the predicted probability of being treated given the covariates.17
The propensity score can then be used to estimate the treatment effect in various ways. Typical strategies include comparing those whose propensity score is similar, such as propensity score matching, or by constructing synthetic populations by weighting observations, such as inverse probability of treatment weighting (IPTW).18,19
Doubly-robust estimation, an interesting related method, combines two modeling approaches—g-computation and IPTW—to obtain one treatment effect estimate, such that the estimate is consistent if one of the two models is correctly specified (which is still a substantial ask).20

Another very typical causal inference approach, named the regression discontinuity method, involves looking at discontinuities in regression lines at the point where an intervention takes place.22 As an example, we might look at how different levels of dynamic pricing influence customers’ decisions to request a trip on the Uber platform. Figure 4 above illustrates this type of analysis.
The idea here is that, in the absence of a causal effect, trip request rates should be very similar on different sides of a sharp cut-off point, such as a specific surge level. This holds true if we can assume that the riders who are very close to the cut-off point are similar with respect to any relevant confounding variables. If this assumption holds and there is a clear discontinuity in trip request rates at the cut-off point, this is evidence that crossing the surge cut-off point has a causal impact on request rates.
A variation of this approach is to look at time series data of some outcome of interest before and after a candidate causal event. This approach is known as the interrupted time series design. Here, the goal is to estimate whether there is a change in the time series at the time the event takes place. The methods we typically use are based on synthetic control and Bayesian structural time series approaches.23,24
A related method that we have used successfully at Uber, the difference-in-differences analysis, looks at the difference in outcomes between those who are treated and those who are not treated before and after the treatment of interest takes place.25,26 The assumption here is that if the treatment influences the outcome of interest, then there should be a change in the difference between those who are treated and those who are not, from before to after the intervention. A typical use case for these types of methods is a marketing campaign or a new product feature that is launched in a particular city.
The instrumental variables approach, a final family of observational methods frequently used at Uber, allows us to estimate the effect of a candidate cause on an outcome if we are able to identify a third variable, known as the instrument, whose influence on the outcome goes through the candidate cause, as depicted in Figure 5, below:

Continuing the Uber Eats example from above, we still have the potential back-door path between the delayed deliveries and customer engagement, which could bias our estimate. However, if we are able to identify some third variable that is only related to the outcome of interest through experiences of delayed deliveries, then we can use that variable to estimate the impact of delayed deliveries on the outcome.
Defining the third variable is a difficult task that often requires substantial knowledge of the particular situation. In this case, a certain type of bug or outage could satisfy the conditions for an instrument. A related but lesser-known strategy is the front-door approach, where researchers are able to estimate the effect of a variable if the relationship between that variable and the outcome of interest is entirely mediated by some intervening variable, along with certain other conditions.
While these methods for observational causal inference have proved very useful in practice, they must be used with caution because their validity rests on certain untestable assumptions. As an example, a consistent estimation of the treatment effect using propensity score matching requires that all relevant confounding variables be included in the propensity score model. However, it is not easy to determine whether or not this assumption holds.
One practical way in which we have sought to address this problem is by using graphical causal models, such as the one leveraged in the Uber Eats customer engagement model, which encode the underlying assumptions in a transparent manner.2,27 Together with substantial domain knowledge, using such graphs has helped us evaluate the plausibility of our models. Additionally, we have used approaches such as sensitivity analysis and simulated tests with known causal effects.28
Future directions for causal inference
In recent years, causal inference has become an active research area in the field of machine learning.29,30 Influential applications include the estimation of counterfactuals in time series data and determining heterogeneous treatment effects in experiments.31 Many of the approaches that combine causal inference and machine learning are motivated by the idea of bringing a large number of covariates to bear on traditional causal inference problems.
At Uber, we’re developing many kinds of causal inference solutions that will help us answer questions that are relevant to our business. To scale causal inference methods, we’re building such approaches into platforms and tools that can be easily used by teams across the company. In the machine learning front, we’ve implemented a number of cutting edge uplift modeling algorithms in a Python package, which helps data scientists and analysts find optimal treatment group allocations in experiments. In parallel with the development of platforms and tools, we’ve also formed a causal inference community at Uber to facilitate learning and sharing, as well as advocate for analysis best practices.
The header image for this article was generated via wordclouds.com.
References
- Morris WE, Brown CR. David Hume [Internet]. Spring 2017. Zalta EN, editor. The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University; 2017. Available: https://plato.stanford.edu/archives/spr2017/entries/hume/
- Pearl J. Causality: Models, Reasoning and Inference. 2nd ed. New York, NY, USA: Cambridge University Press; 2009.
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. J Educ Psychol. 1974;66: 688–701.
- Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search. 1993;81. doi:10.1007/978-1-4612-2748-9
- Deng A, Xu Y, Kohavi R, Walker T. Improving the Sensitivity of Online Controlled Experiments by Utilizing Pre-experiment Data. Proceedings of the Sixth ACM International Conference on Web Search and Data Mining. New York, NY, USA: ACM; 2013. pp. 123–132.
- Angrist JD, Imbens GW, Rubin DB. Identification of Causal Effects Using Instrumental Variables. J Am Stat Assoc. Taylor & Francis; 1996;91: 444–455.
- Imbens G. Methods for Estimating Treatment Effects IV: Instrumental Variables and Local Average Treatment Effects. Technical report, Lecture Notes 2, Local Average Treatment Effects, Impact Evaluation Network, Miami; 2010.
- Peck J, Childers TL. Individual Differences in Haptic Information Processing: The “Need for Touch” Scale. J Consum Res. Narnia; 2003;30: 430–442.
- Bloch PH, Brunel FF, Arnold TJ. Individual Differences in the Centrality of Visual Product Aesthetics: Concept and Measurement. J Consum Res. Narnia; 2003;29: 551–565.
- Allenby GM, Rossi PE. Marketing models of consumer heterogeneity. J Econom. 1998;89: 57–78.
- Schwartz B, Ward A, Monterosso J, Lyubomirsky S, White K, Lehman DR. Maximizing versus satisficing: happiness is a matter of choice. J Pers Soc Psychol. 2002;83: 1178–1197.
- Parker AM, De Bruin WB, Fischhoff B. Maximizers versus satisficers: Decision-making styles, competence, and outcomes. Judgm Decis Mak. Society for Judgment & Decision Making; 2007;2: 342.
- Grimmer J, Messing S, Westwood SJ. Estimating Heterogeneous Treatment Effects and the Effects of Heterogeneous Treatments with Ensemble Methods. Polit Anal. Cambridge University Press; 2017;25: 413–434.
- Wager S, Athey S. Estimation and Inference of Heterogeneous Treatment Effects using Random Forests. J Am Stat Assoc. Taylor & Francis; 2018;113: 1228–1242.
- Ascarza E. Retention Futility: Targeting High-Risk Customers Might be Ineffective. J Mark Res. SAGE Publications Inc; 2018;55: 80–98.
- Rzepakowski P, Jaroszewicz S. Decision trees for uplift modeling with single and multiple treatments. Knowl Inf Syst. 2012;32: 303–327.
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. Narnia; 1983;70: 41–55.
- Stuart EA. Matching methods for causal inference: A review and a look forward. Stat Sci. 2010;25: 1–21.
- Austin PC, Stuart EA. Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat Med. 2015;34: 3661–3679.
- Funk MJ, Westreich D, Wiesen C, Stürmer T, Brookhart MA, Davidian M. Doubly robust estimation of causal effects. Am J Epidemiol. 2011;173: 761–767.
- Cohen P, Hahn R, Hall J, Levitt S, Metcalfe R. Using Big Data to Estimate Consumer Surplus: The Case of Uber [Internet]. National Bureau of Economic Research; 2016. doi:10.3386/w22627
- Lee DS, Lemieux T. Regression Discontinuity Designs in Economics. J Econ Lit. 2010;48: 281–355.
- Abadie A, Diamond A, Hainmueller J. Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California’s Tobacco Control Program [Internet]. National Bureau of Economic Research; 2007. doi:10.3386/w12831
- Brodersen KH, Gallusser F, Koehler J, Remy N, Scott SL. Inferring causal impact using Bayesian structural time-series models [Internet]. arXiv [stat.AP]. 2015. Available: http://arxiv.org/abs/1506.00356
- Athey S, Imbens GW. Identification and inference in nonlinear difference-in-differences models. Econometrica. Wiley Online Library; 2006;74: 431–497.
- Abadie A. Semiparametric Difference-in-Differences Estimators. Rev Econ Stud. Narnia; 2005;72: 1–19.
- Steiner PM, Kim Y, Hall CE, Su D. Graphical Models for Quasi-experimental Designs. Sociol Methods Res. 2017;46: 155–188.
- Liu W, Kuramoto SJ, Stuart EA. An introduction to sensitivity analysis for unobserved confounding in nonexperimental prevention research. Prev Sci. 2013;14: 570–580.
- Athey S. The Impact of Machine Learning on Economics.
- Varian HR. Big Data: New Tricks for Econometrics. J Econ Perspect. 2014;28: 3–28.
- Athey S, Tibshirani J, Wager S. Generalized Random Forests [Internet]. arXiv [stat.ME]. 2016. Available: http://arxiv.org/abs/1610.01271

Totte Harinen
Totte Harinen is a senior data scientist with Uber Labs, Uber's Applied Behavioral Science team.

Bonnie Li
Bonnie Li is a senior data scientist with Uber Labs, Uber's Applied Behavioral Science team.
Posted by Totte Harinen, Bonnie Li
Related articles

How LedgerStore Supports Trillions of Indexes at Uber
April 4 / Global
Most popular

Building Scalable, Real-Time Chat to Improve Customer Experience

DragonCrawl: Generative AI for High-Quality Mobile Testing

Network IDS Ruleset Management with Aristotle v2

Load Balancing: Handling Heterogeneous Hardware
Products
Company